Art I Focus Name Two Unusual Aspects of the Interior or Exterior of the Pantheon Dome

The research is conducted in 2 phases. It begins with a study of the full general layout of the coffers relative to the sphere, together with horizontal and vertical orientations of the 28 sectors and v levels. Subsequently, a closer assay of the shape and geometry of the coffers is proposed, providing a set of metric data that have been processed on the footing of the results from the previous survey and proposing design criteria for the construction of the ideal sector of the coffers. The post-obit factors have been considered.

General organization:

• Division of the circumference into 28 equal parts;

• Location of the axes of the bisectors of the sectors;

• Principal axis accurateness;

• Average circumferences passing through the vertex of the coffers: concentricity and orientation;

• Vertical external lines of the convergence of the coffers.

Shape and geometry:

• Analysis of surface geometry;

• Dimensions study: calculation of averages and written report of diminution of dimensions;

• Vertical stripes betwixt sectors and horizontal stripes between levels;

• Convergence of transition surface directions;

• Comparative study of the perspective projection of the coffers;

• Proportion of external and inner shapes of coffer levels.

General Arrangement

The division of the hemisphere into 28 equal parts was difficult to obtain at the fourth dimension of construction. The division of a quarter of the circumference into 7 equal parts was a complicated geometric problem (Martines 1989). Moreover, the setting out on site was peculiarly difficult at the location of the cornice of the vault. The choice of this complex division may be associated with cultural and symbolic reasons (Lucchini 1996: 109; Wilson Jones 2000: 183) or with the special proportions of the coffers adapting to the spherical surface (Saalman 1988: 121).

Pelletti (1989: 17) described the ancient method of dividing a circumference using strings, but stated that it would not have been possible to use this method for the Pantheon's dome due to the telescopic of the projection and the presence of scaffolding structures. Taylor (2006: 199) proposed the hypothesis that the division was made on the flooring and then disassembled and reassembled at the site of the cornice line. This organization immune for a reduction of possible mistakes, but it would also stop construction for a considerable period of fourth dimension. Waddell (2008: 84) put forward a theory about the mathematical division of the circumference into 28 equal parts by using a specific number of Roman feet.

According to the calculations of the nowadays study, the accuracy of the radial distribution of the coffers is surprising (Fig. 5). When observing deviations in the plan between the bisectors of the coffer sectors and the axes that theoretically split the circumference into 28 equal parts, the boilerplate recorded difference barely reaches 0° 36′ (Table one). The angles betwixt vertical axes of the coffer sectors are extremely close to 12° fifty′, which is equivalent to the subdivision of the 360° platonic model into 28 equal parts.

Fig. 5

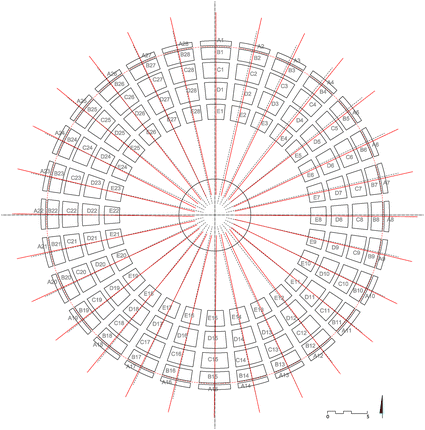
Full general arrangement: analysis of the accurateness of the main axes and of the distribution of bisectors of the sectors

Full size image

Table 1 Angles between the bisectors of the coffer sectors

Total size table

We noted that the axis of the countinghouse sector situated opposite the entry portal is parallel to the Northward–South axis at a altitude of 15 cm. This particular may betoken that the partition of the circumference into 28 equal parts might have been started or completed with this sector.

If we observe the alignment between the sectors of quadrants I and III, nosotros tin meet that the half-dozen opposing countinghouse sectors are perfectly aligned. However, the sectors of quadrants 2 and 4 are not aligned with their opposites. The maximum divergence is registered in the two sectors of quadrants 2 and Four, where the bisectors reach a distance of 39 cm from the centre of the platonic sphere.

Nosotros continued the observation of the general system by studying the main axes in plan view.

The accurateness of the orientation of the North–Due south axis stands out for its precision if we compare it with other Roman buildings with similar dimensions. For example, the Coliseum shows a more pronounced gap in the orthogonal direction of the chief axis (Pelletti 1989: 15). In studying the segmentation of the circumference into four quadrants, it is evident that the longitudinal and transversal axes are approximately orthogonal. Nevertheless, we can also discover that the 4 lines that result slightly diverge from the center of the ideal sphere. The Eastward transversal axis shows a distance from the centre of the sphere of approximately 16 cm and the West transversal axis has a slightly greater value. The two parts show a minimum difference from the perfect orthogonality: 90° 50′ betwixt the East transversal axis and the longitudinal axis; 90° 32′ between the Westward transversal axis and the longitudinal centrality.

Another topic included in this research is the verification of the horizontality of the dissimilar countinghouse levels. The average circumferences following the points defined by horizontal edges generally present a slight slope relative to the horizontal airplane, with an average value of approximately 0° 19′ (Fig. vi). All maximum gradient lines of the planes defined by the circumferences are oriented northwest/southeast.

Fig. 6

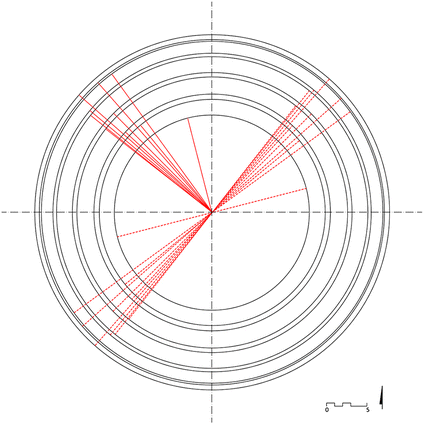
Boilerplate circumferences passing through the external points of the coffers: assay of horizontality and concentricity

Total size epitome

The upper circumference of the last level of the coffers shows a greater inclination than the average value, and it is directed towards the Northward direction. This difference may evidence an actual defect in the pattern construction if compared with the other levels, even if the value is very slight (0° 27′ with the horizontal aeroplane). The average circumferences are approximately concentric. The main altitude between the centre of the circumferences and the centre of the ideal sphere is only 7 cm. These information provide new affidavit of the incredible accuracy of the vault to the ideal model, and also confirms the uniformity of the general distribution of the coffers.

By studying the shape of the vertical sectors, it can be seen that the curves representing the alignments of the external points of the coffers do non converge towards the sphere's pole, as might be assumed (Fig. 7). Based on our written report of the bisectors of the coffers, the sectors tend to converge with high approximation towards the heart of the sphere. The external limits of the coffers might accept been traced from them according to a arrangement based on the accurateness of the bisector pattern.

Fig. seven

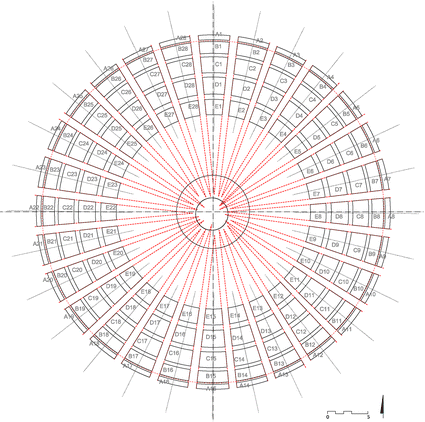
Alignments of the external edges of the coffers showing that they exercise not converge in the upper pole of the sphere

Full size prototype

The extension of these external lines of each sector generates a vertex at a sure distance from the centre of the sphere. The locations of these points do not approximate a circumference but rather prove evident irregularities. If nosotros attempt to establish a relation betwixt this fact and the analysis of the dome surface, it appears that the organisation of the vertexes somehow reflects the presence of plain-featured areas in the North–South zone of the dome. In fact, the vertexes that present the greatest distance from the centre are located in this area.

Shape and Geometry

The continuous reduction of the dimensions and variations in coffer shape, when adapted to the curvature of the sphere, upshot in a harmonious design of the dome soffit. The visual perception of the coffers is influenced by the inner surface proportions and the various directions of the transition surfaces.

The Romans used coffers in barrel vaults, but there are few surviving examples of double-curvature surfaces. One of the most ancient examples is the vault of the sanctuary of Fortuna Primigenia, which dates from the end of the second century B.C. (Lugli 1957: Tav. CCIX). In this case, the coffers have a trapezoidal shape and allow a complete perspective vision adapting to the vault surface.

In the Thermal Baths of Trajan and in the Pantheon, nosotros find the first preserved examples of coffers adapted to a spherical surface (Waddell 2008: 58). Fine Licht (1968: 276) and Wilson Jones (2000: 192) noted the relevance of the perspective design and radial distribution of the coffers of the East room of the Baths, while the remaining structures cannot be evaluated due to their poor country of conservation.

In the Pantheon the coffers that appear square to the eye actually accept a trapezoidal shape. The command of visual effects may be directed to institute a connexion between coffer distribution and the pavement grid, which is composed of large squares. The dimensions of the floor squares are visually like to the prototype of the dome coffers (Waddell 2008: 85) (Fig. 8).

Fig. 8

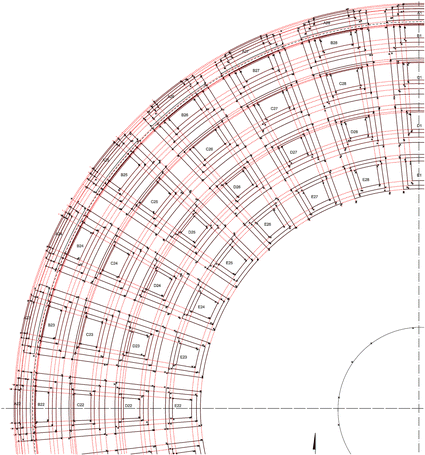
Arrangement of coffers. Study of the alignment through calculated average of the positions of the survey points

Full size image

Many authors, including Fine Licht (1968: 140) and Waddell (2008: 85), have stated that the coffers of the Pantheon's dome do non play a constructive or structural part simply are merely decorative elements. Their function is primarily related to visual perception, which may justify their complex design.

Nosotros began the analysis by studying whether the different surfaces making up the coffers are spherical or flat (Fig. 9). An ideal flat surface was created with successive calculations on each of the intermediate and deepest levels of ane sector of coffers. The distances of the raised point from this flat average surface were minimal (ii–3 cm). It can thus exist deduced that the intermediate and the deepest levels practise not conform to a spherical surface simply tend to be apartment, which would undoubtedly get in easier to control the formwork.

Fig. 9

Photograph of the internal surfaces of the coffers

Total size epitome

One of the dome quadrants was carefully studied: dimensions of six sectors of coffers were recorded, and the data were processed through a calculation of averages to obtain reference values of their measurements. Nosotros drew an orthogonal projection of each coffer of the second sector of the Due north-E quadrant. Even if these projections are orthogonal, they reduce the actual length of the curves due to their restitution onto a airplane. Moreover, we proposed another calculation of the length of the arcs that defines the external edges of the coffers. The values of sectors ii, three, 4, 5 and 6 of the Northward-East quadrant were registered and used to obtain the average values (Tabular array 2).

Table 2 Due north-East quadrant

Total size table

The results prove a gradual decrease of the length of the vertical arcs of the coffers. The boilerplate values from the showtime level (A) to the last level generated a numerical progression:

0.93	0.86	0.75	0.threescore
(B:A)	(C:A)	(D:A)	(E:A)

This progression increased with the upper levels and was related to the unlike perception of the curvature of the vault. The final level of coffers shows the greatest difference with the previous level.

The width of the coffers too progressively decreased every bit they progressed towards the upper levels. The deviation betwixt the upper and lower edges of each coffer increased in the college levels, reflecting the necessity to suit to the spherical curvature. The upper width of the last coffer was approximately one-half of the lower length of the coffers at the first level. The analysis shows that the coffer sector of the North–South centrality opposite from the entrance portal has a major difference in width (the coffer of the starting time level of this sector, named A1, measures iv.00 thou in its lower part, whereas the balance of coffers measure out as follows: A2, 3.90 thousand; A3, 3.94 m; A4, 3.86 m; A5, 3.83 m; A6, 3.86 k; A7, three.85 m; A8, 3.92 chiliad). This difference has an impact on the radial arrangement of the coffers and generates the divergence of the bisector that was registered past the comparison of the survey model and the platonic model. Moreover, every bit in our previous report (Aliberti et al. 2014), the bisector of this sector shows a gap with the North–Southward axis. This divergence from the average value was distributed evenly between the half-dozen sectors of the second quadrant in order to generate a uniform paradigm of the soffit frame.

The results propose that the sectionalization of the circumference into 28 equal parts could non be controlled by rigid geometrical construction; the layout of the coffers was adapted to the slight divergences of the North–Southward sector to determine a uniform distribution using an empirical method. The setting-out on site may accept been performed through a applied-effective technique based on experimentation more than than circuitous geometrical laws.

The depth of the intermediate surfaces changed at different countinghouse levels. Using the section passing through the vertical centrality of the coffer sector, we studied the 2nd sector of the North-East quadrant (Fig. 10). As we can see in Table three, in that location is a small and gradual decrease in depth from the first level to the fifth level. The slight departure recorded between the commencement three internal surfaces measures a maximum of four cm. It is evident that the greatest subtract in depth appears in the last surface. This 4th surface disappears in the upper level of the coffers; therefore, the 3rd surface follows a different design.

Fig. 10

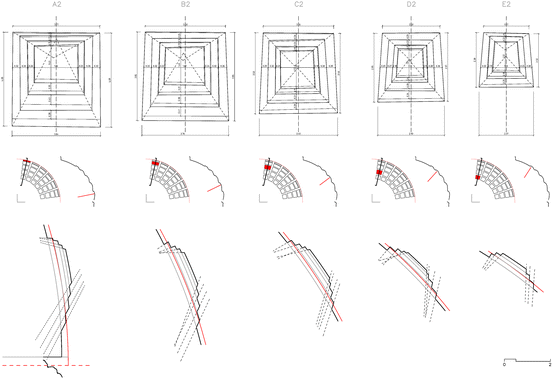
Coffer dimensions. Vertical section and orthogonal project of the coffers of sector two of the North-East quadrant

Full size image

Tabular array iii Northward-East quadrant

Total size tabular array

Unlike the countinghouse width and height variations, the horizontal bands separating the coffers have very similar dimensions. When calculating these values as arcs of a sphere, the average value is 0.84, with variations of a few centimetres between zones. This regularity is besides reflected in the separation between the vertical sectors of the coffers. Based on the written report of the North-East quadrant, the average distance between the lowest external points of the first level is 1.02 grand, which becomes 0.67 betwixt the upper external points of the last level. According to these information, the meridian rib is reduced to almost half of its width from showtime to end, a fact that is not perceived from the overall view of the dome, where these strips appear to accept near uniform dimensions. Nosotros used these studies on the average measurement of coffers and their distribution as a first metrical reference to build the complete platonic model.

In analysing the direction of the transition surfaces between the unlike levels, the radial tracings were identified, and other tracings approximately converged into certain reference points outside the coffers (Fig. 11).

Fig. xi

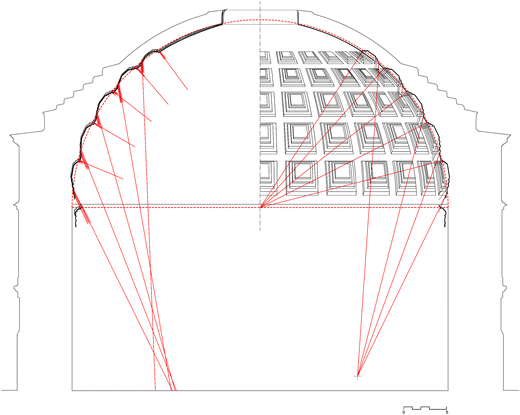
Report of the direction of the transition surfaces: average calculation applied to the rotation of the radial sections and hypothesis of ideal alignment

Full size image

These connecting planes are much shorter than the dimensions of the unabridged dome; therefore, it is difficult to provide an exact definition of their directions. Nevertheless, we can notation that the upper connecting surfaces appear to be orthogonal to the spherical surface of the dome. The junior transition surfaces present a greater inclination in order to open the visual field and leave every edge of the coffers visible.

We interpreted these convergences in the structure of the ideal model (Fig. 12). Here, the upper connecting surfaces were congenital as radial, and the inferior ones converged to a point at a certain distance from the centre. Although the constructed object is non as exact as the ideal model, these convergences indicate that there is a circular zone where a viewer can see all the inferior edges of the coffers and nigh all the upper edges.

Fig. 12

View of the complete ideal model as result of the geometrical analysis

Full size paradigm

In studying this subject, we should consider that the results are based on the current country of the coffers registered past the signal cloud. They may have been slightly modified by the cladding restoration works of Terenzio (1933) in the 1930s and more recently of Belardi (2006), especially if we refer to the smallest surfaces.

The coffer arrangement allows complete visibility from the centre of the floor. This ascertainment has been verified through the study of the point cloud generated from the eye of the room without because scannings performed on the transversal and longitudinal axes. This unique point cloud perfectly describes every part of the coffers and their complex surfaces without detecting any blind areas. The present enquiry, performed with sophisticated devices and software, verifies the aggressive work of the Roman builders based on empirical knowledge of perception and geometry and carried out with the apply of ancient tools.

To perform specific studies of the coffer design, a set up of alignments was fatigued employing tools that utilize average calculations. The drawing of the diagonal lines connecting the external vertices of each coffer's transition surface was uniformly repeated in all of the sectors (Fig. 13). There was a progressive variation in the inclination of the diagonals, which in the get-go levels clearly pointed towards the upper part of the coffers and gradually declined in the last levels.

Fig. xiii

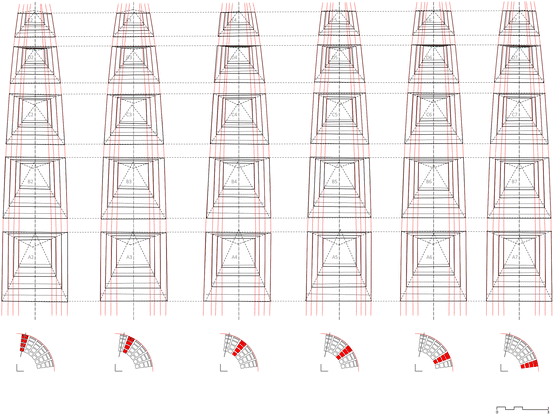
Elevation of each coffer sector of the Northward-East quadrant. Written report of alignment and proportions

Full size image

To capeesh the perspective attributes of the coffers, a serial of projections was performed from dissimilar points of view. By comparison dissimilar perspective views, information technology tin exist directly noted how the perception of these elements slowly changes.

We began the report past generating a frontal perspective view of each coffer of the second sector of the N-East quadrant. The indicate of view was located in the middle of the room and at a man's height of 1.70 m. It is axiomatic that this perspective view reproduces an almost square image, and the coffer surfaces seem to be regular and of the same dimensions. The perceptive differences of the coffer parts are not visible from the middle of the room.

Each coffer generates a different image when the inclination of the perspective axis moves, thus showing its trapezoidal shape. Creating the epitome of a pure shape, such as a square, is part of the search for regular forms present in the classical Roman culture (Fernández-Cabo 2013: 543). This image of a square may be associated with the external shape of the coffers, while the inner levels show some differences (Fig. xiv).

Fig. fourteen

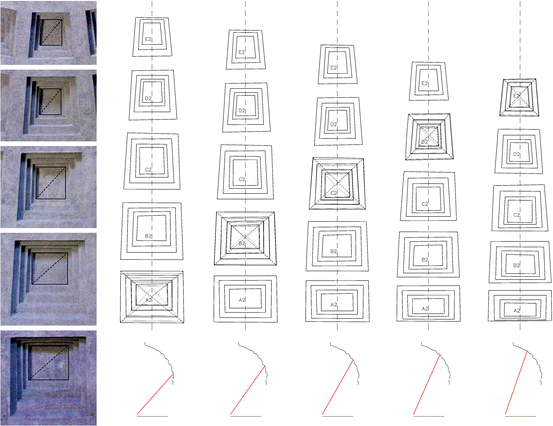
Study of the proportions of the inner levels applied on the survey model orthogonal views and perspective projection from the centre of the room of the coffers of the North-East quadrant

Full size image

If nosotros approximate the course of the inner levels of the coffers to rectangles, information technology is evident that their proportions alter from the horizontal to the vertical. This change is probably a outcome of ii conditions of coffer design: the aim to preserve the vertical alignment of the sector in the width of both the external and internal levels; and the need for greater alteration of the lowest coffers to command the perspective view from the eye of the room. The lowest connecting planes in the kickoff two levels of the coffers are larger than in the upper levels and the inner figure is thus a horizontal rectangle. From the third level to the fifth, the inner figure is a vertical rectangle. Moreover, the differences between the 2d and the third level are greater than between the residuum of the levels, so the transition seems not to be completely compatible. In whatsoever case, it is highly relevant that these rectangles with different proportions are approximately centred in a perspective view from the centre of the room.

Based on these studies, we can state that the pattern of the inner levels of the coffers seems not to depend on the projection from a hypothetical point, in dissimilarity with some scientific studies. We consider that from the bespeak of view of construction, such a dependence would be very hard to achieve due to the great altitude and the height of the dome from the floor. Furthermore, as far every bit we currently know, in ancient times there was no knowledge of the perspective method or of spherical geometry.

giorzacande1979.blogspot.com

Source: https://link.springer.com/article/10.1007/s00004-017-0339-7

Share this post